Les 288.982 premières décimales du nombre de Champernowne « premier », par Jean-François Colonna
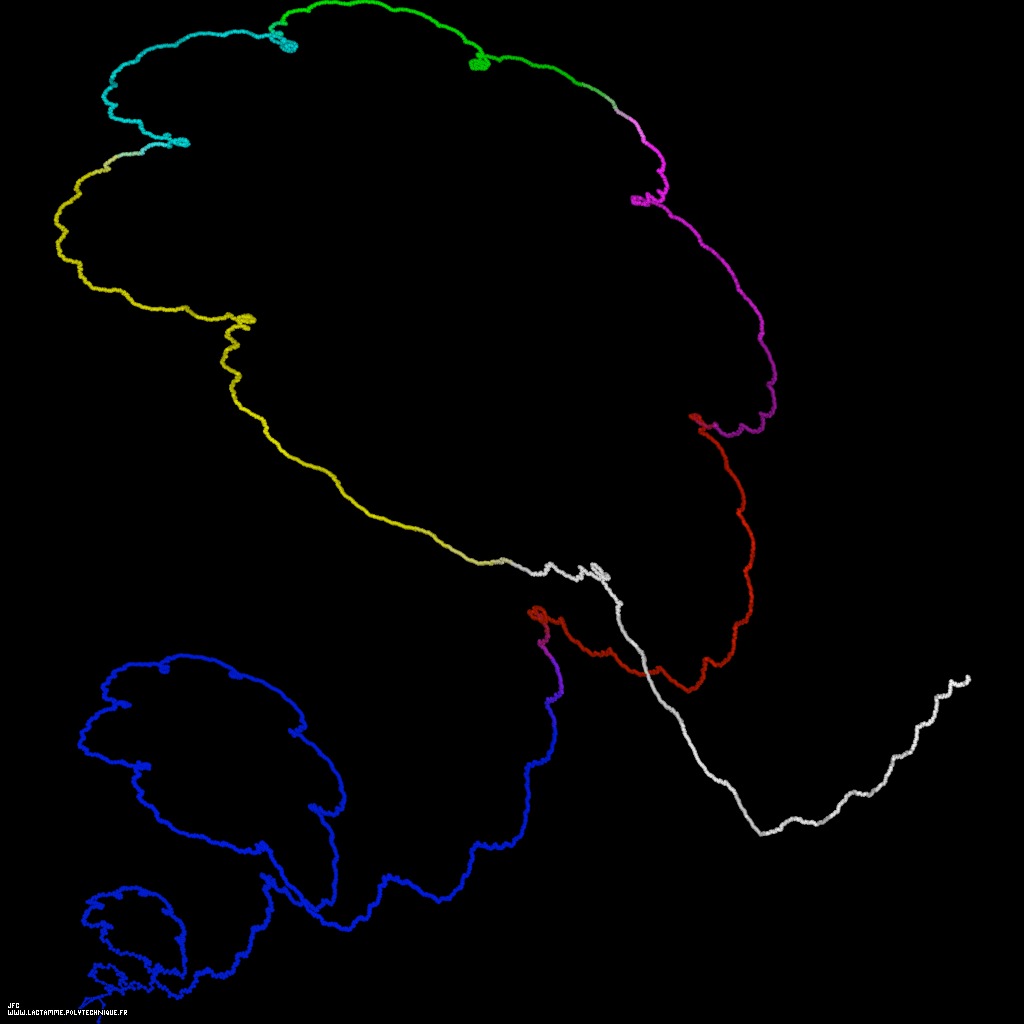
Les 288.982 premières décimales du nombre de Champernowne « premier » ( = 0.2 3 5 7 11 13 17 19 23 29...) visualisées comme une marche aléatoire bidimensionnelle « absolue » en utilisant la racine carrée de la distance à l’origine
Crédits : Jean-François Colonna, http://www.lactamme.polytechnique.fr/Mosaic/images/CHAM.61.D/display.html
Voir d'autres images du jour.
Ressources pédagogiques
-
le 7 mai 2024Nous découvrirons ici de quelle manière Vladimir Berkovich fit ses premiers pas dans les arbres.lire l'article
-
le 2 mai 2024Enfant j’avais été impressionné par cette boîte de conserve qui différait des boîtes cylindriques habituelles.lire l'article
Actualités des maths
-
18 décembre 2023Séminaire « Mathématiques et poésie, le fond et la forme » 7e séance le mercredi 20 décembre 2023
-
12 décembre 2023Séminaire « Mathématiques et poésie, le fond et la forme » 6e séance le mercredi 13 décembre 2023
-
4 décembre 2023Séminaire « Mathématiques et poésie, le fond et la forme » 5e séance le mercredi 6 décembre 2023
-
20 novembre 2023Séminaire « Mathématiques et poésie, le fond et la forme » 4e séance le mercredi 22 novembre 2023
-
13 novembre 2023Séminaire « Mathématiques et poésie, le fond et la forme » 3e séance le mercredi 15 novembre 2023
-
6 novembre 2023Journée Tangente 2023 le 3 décembre 2023